PORTLAND – It wouldn’t be unsafe to say that our education system in the United States is at least a couple of years behind systems in countries that are leading in education.
Our system needs a major jolt and revival to a new life. The new school grading in Maine is a step in the right direction, done with good intentions — but, sadly, with a blindfold.
The formula for calculating recent high school grades is a classic example of mediocre mathematics.
INEXACT RANKINGS HAVE BIG IMPACT
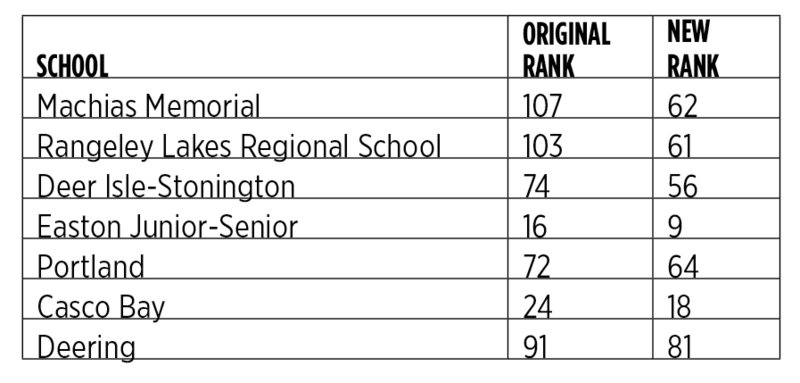
The metric is so extremely inconsistent that when it’s slightly modified, it causes dramatic movement of anywhere from 10 to 45 moves in the rank of a school, i.e., a school that is originally ranked 100 may actually come down to 55. This may change the school’s grade from an F to a C or even a B.
The top 35 schools are rock solid and do not move much in ranking, no matter what variations are made to the metric.
The next 50 schools move three to nine places depending upon only slight changes in the metric, while the biggest shift takes place in the bottom 50 schools.
Incorrectly ranking the schools with inferior grades has a much bigger negative impact than ranking the superior schools correctly.
In the current system, where every school is considered the same irrespective of their size, it is likely that the resources propelled into the low-performing schools will be far from optimal. There is a higher likelihood of disproportionately spending funds and resources on schools that probably don’t need it, throwing the schools that actually need support further down the drain.
The problems with the current grading system are multifold.
SAME TYPE OF DATA COUNTED TWICE
First, the same factors associated with higher grades are used multiple times in the algorithm, or calculation formula, to create a total score of excellence.
High schools were graded on two principal domains: proficiency and progress.
Proficiency was broken down into math and reading. Progress was broken down into four parts: math and reading progress, and four- and five- year graduation rates.
The problem lies in the intrinsic high correlation between these six criteria. Statistical modeling techniques warn against using a single piece of information more than once in an estimation.
For example, imagine a dataset of ages. If 10 is added to all those ages, then the new set of numbers will not give any additional information about the original data. The two will be perfectly correlated with each other. This phenomenon — known as multicollinearity — makes estimates sensitive to small changes in value. The current grading system is severely suffering from the problem of multicollinearity.
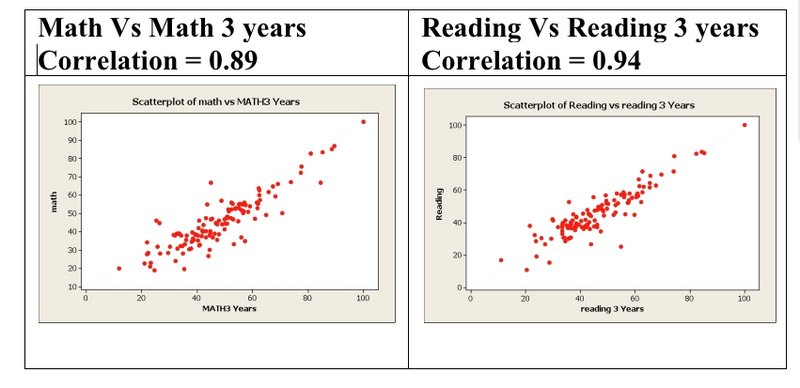
The concept of high correlations is shown in the scatterplot graphic above with the data that was used for grading.
Data shows that schools that achieve high math proficiency scores one year also have high three-year math scores. If a school has a high math proficiency rate, then it is extremely likely to have a three-year running average of high math proficiency as well. The same is true of the results for reading outcomes.
Surprisingly, these correlated criteria were used independently in the algorithm. A school with a lower math score is essentially punished doubly in this algorithm, and a school with a higher score is rewarded doubly. While analyzing the data, I found that minor modifications — such as not punishing schools twice for the same criteria — result in a noticeably different set of rankings. The table above offers examples of how schools moved in the rankings.
KEY VARIABLES IGNORED
Second, important aspects that might make or break learning outcomes for a school were ignored.
Factors such as student-teacher ratio, teacher qualifications and salary, the socioeconomic status of the town, science proficiency, student demographics, etc., are important predictors of learning environment for a school, which were not considered.
LOCATION, LOCATION, LOCATION
Third, all high schools, no matter where they were located in the state, were compared equally. This had a huge impact on the grading algorithm.
A comparison between a high school in a small town up north with schools in the Portland area will be unfair. A small-town school is more likely to be deficient in resources compared to a school in a larger town or city.
As a consequence, schools that are ranked very low with poor grades really have no silver lining to hope for.
Is there a better solution? This is not all about pinpointing mistakes, but also about offering a better, viable solution.
My recommendation would be to make it a fair, meaningful and numerically correct system.
NCAA SYSTEM: A ROLE MODEL
A sound grading system could learn from the NCAA sports championships, dividing schools into divisions based on similarity of their characteristics.
These divisions could be created based on a single principle: Schools within a division will be similar to each other, and divisions will be dissimilar from each other. A tangible benefit of this kind of divisional clustering is the proportionate and proper allocation of resources.
It will take off the pressure and unintended humiliation that schools may have suffered after the rankings were announced. And it would give them a chance to grow slowly and steadily. That would be a fair way of ranking schools and would give schools the most important ingredient to work harder: hope.
Incidentally, a group of four graduate students has been working on a similar algorithm under my supervision as part of the requirement for a course titled “Probability and Statistics.” The state grading system could not have come at a better time, as we are getting ready with a much better, statistically sound and robust algorithm to rank and grade high schools.
Prashant Mittal (email: pmittal@usm.maine.edu) is a senior statistician at the University of Southern Maine and teaches applied statistics and data analytics courses at the USM School of Business.
Copy the Story LinkSend questions/comments to the editors.

Success. Please wait for the page to reload. If the page does not reload within 5 seconds, please refresh the page.
Enter your email and password to access comments.
Hi, to comment on stories you must . This profile is in addition to your subscription and website login.
Already have a commenting profile? .
Invalid username/password.
Please check your email to confirm and complete your registration.
Only subscribers are eligible to post comments. Please subscribe or login first for digital access. Here’s why.
Use the form below to reset your password. When you've submitted your account email, we will send an email with a reset code.